Since 
represents the energy and momentum content of the fluid,
there must be some way of using it to express the law of conservation of
energy and momentum. In fact it is reasonably easy.
Consider a cubical fluid element [ see Figure 4.1 ] of side a, seen only in cross section [ z direction suppressed ].
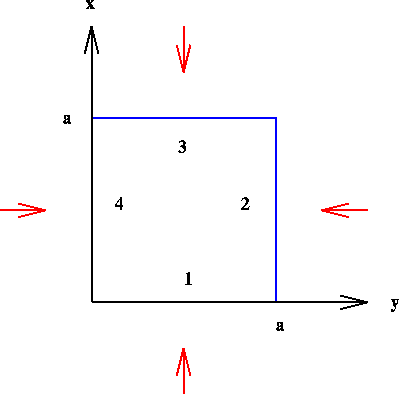
Figure 4.1: Energy flow across a fluid element.
Energy can flow across all sides.
The rate of flow across face (4) is
, and across (2) is 
; the second term
has a minus sign because 
represents energy flowing in the positive
x- direction, which is out of the volume across face (2). Similarly, the
energy flowing in the y direction is 
.
The sum of these rates across each face must be equal to the rate of increase
of energy inside the cube 
: This is the statement
of conservation of energy. Therefore we have:
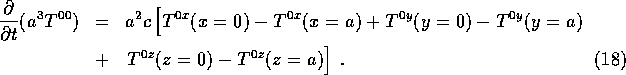
Dividing by 
and taking the limit 
gives
Dividing by c we get
Since 
, 
, 
and 
, we can write this as
or
This is the statement of the law of conservation of energy.
Similarly momentum is conserved. The same mathematics applies, with the index 0 changed to i [ the spatial components ] i.e.
The general conservation law of energy and momentum is therefore
This applies to any material in Special Relativity.